6.1 Raytracing

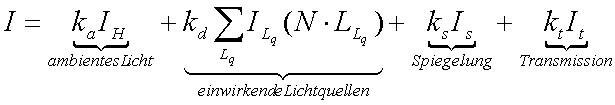6.1.1 Einführung

Das Raytracingverfahren war das erste Beleuchtungsmodell, das die Interaktion zwischen Objekten berücksichtigt. Diese Modelle werden globale Beleuchtungsmodelle genannt. Bilder, die mit diesem Verfahren berechnet werden, erkennt man zum einen an den glänzenden und spiegelnden Oberflächen und zum anderen an den Schlagschatten, die durch Punktlichtquellen mit scharfen Rändern erzeugt werden.

Die Grundidee des Raytracings ist die Umkehrung des Sehprozesses. Physisch werden Photonen von einer Lichtquelle ausgesandt. Kleine Mengen dieser Teilchen gelangen direkt, oder durch Reflexion in das menschliche Auge, wo die Schwingungsenergie der Teilchen, an das Gehirn weitergeleitet, als Farbwert interpretiert wird. Ein einfaches Modell simuliert diesen Vorgang, indem es die von der Lichtquelle ausgesandten Photonen als Lichtstrahl verfolgt. Dieses Verfahren wäre sehr rechenaufwändig, weil auch solche Lichtstrahlen verfolgt werden, die nicht das Auge des Betrachters treffen. Aus diesem Grund wird nicht der Lichtstrahl verfolgt, sondern der Sehstrahl vom Betrachtungspunkt.

6.1.2 Das Verfahren

Bei dem Verfahren von Witthed wird von einem Betrachtungspunkt aus jeweils ein Sehstrahl durch jedes Pixel der Bildebene gelegt (s. Abbildung 1). Trifft der Sehstrahl auf ein Objekt, so bestimmen die vorhandenen Lichtquellen und die Objektoberfläche die Farbe des Pixels. Um den Anteil jeder Lichtquelle für den Punkt auf der Oberfläche zu bestimmen, wird zu jeder Lichtquelle ein Strahl gesendet. Trifft dieser genannte Strahl auf ein dazwischen liegendes Objekt, so wird die Lichtquelle nicht in die Intensitätsberechnung mit einbezogen, da der Oberflächenpunkt von ihr nicht direkt beleuchtet wird.

Abbildung 1

Für die Intensitätsberechnung muss der Oberflächentyp berücksichtigt werden. Es werden drei Arten von Oberflächen unterschieden :

• Matte Oberflächen

• Spiegelnde Oberflächen

• Transparente Oberflächen

Bei matten Oberflächen wird die Intensität durch Addition der erreichbaren Lichtquellen berechnet.
Handelt es sich um einen spiegelnden Oberflächentyp, so wird der Reflexionsstrahl ermittelt und rekursiv weiterbearbeitet. Trifft der Sehstrahl auf ein transparentes Objekt, wird zusätzlich zum Reflexionsstrahl noch der gebrochene Strahl (Transparenzstrahl) bestimmt und ebenfalls rekursiv weiterbearbeitet. Bei transparenten und spiegelnden Oberflächen ergibt sich die resultierende Farbe aus der gewichteten Summe der rekursiv berechneten Intensitäten. In dieser Berechnung wird die Entfernung der Lichtquelle, also der zurückgelegte Weg des Sehstrahl berücksichtigt.
Der Algorithmus terminiert, wenn ein Sehstrahl die Szene verlässt, der Beitrag einer Lichtquelle einen Schwellwert unterschreitet oder eine maximale Rekursionstiefe ereicht ist. Abbildung 2 veranschaulicht dieses Verfahren.

Abbildung 2

6.1.3 Beleuchtungmodell von Whitted

Zur Intensitätsberechnung an den Objektoberflächen wird das von Whitted beschriebene Beleuchtungsmodell benutzt.

(6.1)

Trifft der Sehstrahl auf ein Objekt im Punkt P, so wird die Intensität an diesem Punkt durch die Gleichung 6.1 berechnet (Abbildung 3). Die ersten beiden Terme entsprechen der Schattierungsfunktion des Lambertreflektierers . Die anderen zwei Terme bestimmen den spiegelnden und den durch Transmission einwirkenden Intensitätsbeitrag. Zur Darstellung eines Grauwertbildes auf dem Bildschirm, werden die berechneten Intensitäten auf ganzzahlige Werte zwischen 0 und 255 abgebildet. Sollen Farbbilder berechnet werden, muss die Gleichung 6.1 auf die drei Primärfarben Rot, Grün und Blau angewendet werden.

Abbildung 3

Tabelle 1 zeigt die verwendeten Parameter im Detail :

	Intensität im Oberflächenpunkt P in Richtung des Sehstrahls
	Intensität des reflektierten Lichtes in P
	Intensität des transmittierten Lichts in P
	Normalvektor im Punkt P
	Intensität der Lichtquelle Lq
	Richtung von P zur Lichtquelle Lq
	Intensität des ambienten Lichtes
	ambienter Reflexionskoeffizient
	diffuser Reflexionskoeffizient
	spiegelnder Reflexionskoeffizient
	Transmissionskoeffizient

6.1.4 Verbesserungen

Das Resultat dieser Berechnung lässt sich noch verbessern, indem der Spiegelungsterm um das Beleuchtungsmodell von Phong erweitert wird. Die folgende Gleichung berücksichtigt die Spiegelung nach Phong mit dem lokalen Reflexionsvektor R und dem Vektor A zum Betrachter.

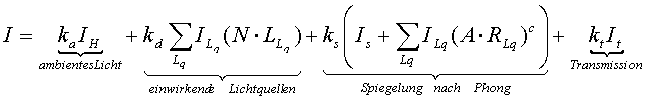
Der Strahlenverfolgungsalgorithmus ist in seiner bis jetzt beschriebenen Form sehr anfällig für Diskretisierungsfehler, da kleine Objekte möglicherweise nicht erfasst werde, bzw. Objektkanten ungenau dargestellt werden. Um diesen Effekt zu reduzieren, werden mehrere Sehstrahlen durch ein Pixel (z.B. 3 x 3 Strahlen) geschickt (super sampling). Die Farbe des Pixels wird durch anschließende Mittelwertbildung der Sehstrahlen bestimmt.
Whitted hat seinen Algorithmus dadurch verbessert, dass er die Sehstrahlen durch die Eckpunkte des Pixelquadrates schickt und die Intensität durch Mittelwertbildung der vier Sehstrahlen berechnet. Der Mehraufwand für diese Methode beläuft sich bei einer Pixelanzahl von s*z Pixeln auf einen linearen Zuwachs von s+z+1 Sehstrahlen.